圆柱螺旋弹簧设计计算

圆柱螺旋弹簧设计计算，属于Myfuntion自定义函数系列。包括弹簧类型有：压缩弹簧（两端燕紧磨平）、拉伸弹簧（圆钩环）！不同的钢丝、不同的圈数、不同的直径组合在一起都能设计出K=400左右的圆柱螺旋弹簧。具体尺寸要通过使用环境来确定。

圆柱螺旋弹簧

K=G*d^4/8/D^3/n

其中G为钢丝的抗剪切模量，d为钢丝直径，D为弹簧中径，n为弹簧有效圈数。

根据此公式，推算设计圆柱弹簧，G的值是各种弹簧钢丝的抗剪模量，通过手册查。

圆柱拉、压螺旋弹簧的设计计算：

1.圆柱螺旋弹簧的主要参数和几何尺寸计算

图15-7 圆柱螺旋弹簧的主要参数

圆柱螺旋弹簧的主要参数（见图15-7），有：
弹簧丝直径d：d增大，弹簧强度提高。
   　　弹簧圈中径D：
   　　弹簧指数C（又称旋绕比）：一般 c=4～16，C小的弹簧刚度大。

（1５－5）    
内径D1：    
外径D2：

弹簧节距p
螺旋升角α。
圆柱压缩和拉伸弹簧的几何尺寸计算见表15-2 。

表15-２　圆柱压缩和拉伸弹簧的几何尺寸计算！

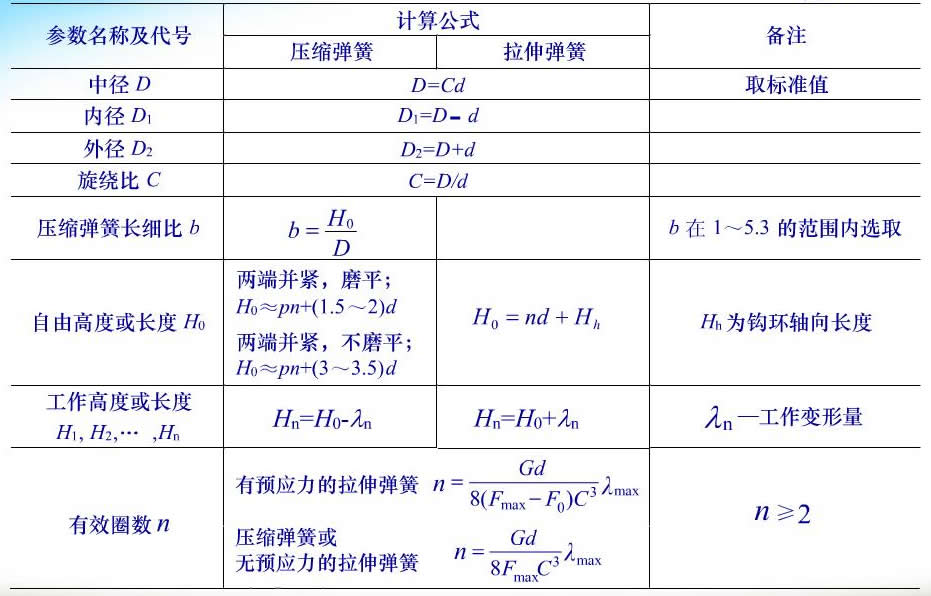
2.弹簧特性线
表示弹簧载荷与变形之间的关系曲线称为弹簧的特性线。设计弹簧时，必须使其工作应力在弹性极限范围内。
圆柱螺旋压缩弹簧的特性线如图15-8 所示。

图15-8 圆柱螺旋压缩弹簧的特性曲线

预紧力F1称为弹簧的最小载荷；F2为弹簧所承受的最大工作载荷，此时，弹簧高度压缩到H2，相应变形为λ2，该时刻弹簧各圈之间仍应保留δ1的间隙，称余隙；Fmax为弹簧的极限载荷，通常应保证F2≤0.8Fmax。λ2与λ1之差或H2与H1之差，称为弹簧的工作行程h。

3、圆柱螺旋拉、压弹簧的设计计算
计算准则：①强度条件；②刚度条件；③稳定性条件。
1.强度计算
   　　    通过弹簧轴线的弹簧丝截面为椭圆，如图15-9所示。因为螺旋升角α很小，约5°至9°，所以，弹簧截面近似圆形。

图15-9 圆柱螺旋压缩弹簧的受力及应力分析
将轴向载荷F向剖面中心简化，则弹簧丝上有扭矩T和力F作用！

（15－6）

（15－7）
叠加后内侧的最大应力为：

（15－8）
考虑弹簧丝曲率和剪切应力对扭切应力的影响， 引入曲度系数K

（15－9）    
有

（15－10）
所以，根据强度条件确定弹簧丝直径ｄ的公式是    

（15－11）

因为［τ］、C都与弹簧丝直径d有关，设计时先估计d，查表15-3得C，查表15-1得［τ］，再按上式确定d，若与估计值不相符，要重新选择d。要求强度求出的d小于估计的d。

表15-3 圆柱螺旋弹簧C的推荐值

弹簧丝直径ｄ／ｍｍ
0.2～0.4
0.5～1.0
1.1～1.2
2.5～6
7～16
18～50
弹簧指数Ｃ
7～14
5～12
5～10
4～9
4～8
4～6

承受变载荷的螺旋弹簧的疲劳强度计算,请参见有关资料。
2.弹簧的刚度计算
   根据力学知识，无预紧力的圆柱压缩（拉伸）弹簧受载后的变形量是

mm
（15－12）

弹簧刚度是表征弹簧性能的主要参数之一，弹簧刚度ｋ为

（15－13）

从上式可以看出，Ｃ值对刚度的影响很大。合理选择旋绕比Ｃ值就可以控制弹簧的弹力。弹簧的圈数根据需要的变形量确定，已知力及变形量，弹簧圈数ｎ为

（15－14）

有预紧力的弹簧变形量和圈数计算见教材或有关资料。
   　　    3.弹簧的稳定性验算
   压缩弹簧的自由高度H0与中径D之比称为长细比，以b表示。

（15－15）    

建议：当弹簧两端固定时，b<5.3；当弹簧一端固定，一端可转时，b<3.7；当弹簧两端都可转动时，b<2.6。   当b大于上述数值时，要进行弹簧稳定性计算。临界稳定载荷

Fc=CｕkH0 N
（15－16）

式中：Fc——临界稳定载荷；Cｕ——不稳定系数；k——弹簧刚度。
  　　为保证弹簧的稳定性必须满足：

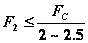
（15－17）

如不满足，应采取以下措施：
  　　（１）改变b值，提高Fc值，以保证弹簧的稳定性；
  　　（２）加装导杆或导套，如图15-10。